Morphological Filters

All Morphological filters are based on two operations -- dilation and erosion . They are defined in the following way. Suppose you have two accidental set of points in discrete two dimensional space: $\{(m,n)\}$ and $\{(p,q)\}$. Lets define a function for these two sets $A(m,n)$ and $B(m,n)$, which we will call as objects $A$ and $B$. The operation dilation (extension) will be defined as following:

$$D(A,B)(r,s)=\max_{(j,k)\in B}(A(r-j,s-k)+B(j,k))$$

Operation erosion looks as following:

$$E(A,B)(r,s)=\min_{(j,k)\in B}(A(r+j,s+k)-B(j,k))$$

It is common to call in the above expressions $A$ as an image, and $B$ as a structural element. The surface plays the role of the image in the morphological filters used in FemtoScan program (lets define it as $S$), while the object $F$ (shown below) most often plays the role of structural element.

$$F=\left\vert\begin{array}{ccc} 0 & 1 & 0 \\ 1 & 3 & 1 \\ 0 & 1 & 0 \end{array}\right\vert$$

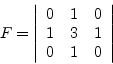
The value 3 correspond to the coordinate $(0,0)$.

Standard morphological filters available in the FemtoScan program and their description are shown in the Table 3.3.

Table 3.3: Standard morphological filters realized in FemtoScan

Filter	Description
Smooth	$Smooth(S,F)=Close(Open(S,F),F)=E(D(D(E(S,F),F),F),F)$
Contrast	$Contrast(m,n)=\frac{D(m,n)-E(m,n)}{65535}\cdot(S(m,n)-E(m,n))$ -- structural element $F$ is used here during the calculation of dilation and erosion .
Min	The new value for the point is taken as minimal one among the value of this point and eight neighbor points. In the terms of morphological operations -- this is an operation erosion with a structural element $3\times3$, where all the value are equal to zero
Max	The new value for the point is taken as maximal one among the value of this point and eight neighbor points. In the terms of morphological operations -- this is an operationdilation with a structural element $3\times3$, where all the values are equal to zero.
Dilate	Operation dilation with structural element $F$.
Erode	Operation erosion with structural element $F$.
Open	$Open=D(E(S,F),F)$
Close	$Close=E(D(S,F),F)$
Gradient	$Gradient=\frac{1}{2}(D(S,F)-E(S,F))$
Laplace	$Laplace=\frac{1}{2}[(D(S,F)-S)-(S-E(S,F))]=\frac{1}{2}[D(S,F)+E(S,F)-2\cdot S]$

Besides traditional morphological filters the program contains the filters specially designed for scanning probe microscopy. For details about this filters please refer to the articles by J.S.Villarrubia, Surface Science 321 (1994) 287-300 and J.S.Villarrubia, J. Res. Natl. Inst. Stand. Technol. 102 (1997) 425.

The calculation of tip of maximal blunt shape which will not put distortions into the image (or a selected part of the image) during tip scanning is launched by the Command Non-distorting tip. In other words it is so as if it is regarded, that the obtained image is a precise copy of the scanned surface and one try to find the tip which can perform such an exact scanning.

The filter Blind tip estimation also calculates the tip of the maximal blunt shape, which can be used for obtaining this image (or a part of it). But the condition on non-distortion is absent now. There is a new restriction on the tip shape. It is quite reasonable, that if the tip apex is of some curvature, then on the image will never appear the protrusion with less curvature. Thus the protrusions are the limitation for the tip shape.

The window with progress indicator appears after the launch of Blind tip estimation filter. The iterations are performed during the filter operation and it is expected, that once the result of the next iteration will be the same as the previous one. The filter operation is stopped when no changes in the tip shape occurs during the iteration. It is possible to stop the filter operation in advance. Press Cancel in the Window of the launched filter to stop the filter operation. You will the shape of the tip for the iteration processed when the button Cancel was pressed.

By command Continue blind tip estimation... the window with list of all open in the program surface images appear. Please select the window, where the tip shape estimation is already stored and press Select. The algorithm of this filter is the same with a little difference, that the initial iteration will not be a plane but the selected shape estimation.

By command Erode tip... The window appears, in which it is necessary to select tip shape estimation among all opened in the program. The filter fulfill the operation erosion over the current image using a selected tip as a structural element.