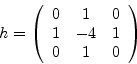В общем виде производная по оси ![]() (оси
(оси ![]() ) для дискретной функции представима
в виде
) для дискретной функции представима
в виде ![]() (
(![]() ), где
), где ![]() обозначает свертку
двух функций,
обозначает свертку
двух функций, ![]() и
и ![]() -- некоторые дискретные функции (матрицы),
-- некоторые дискретные функции (матрицы), ![]() --
дифференцируемая функция. Зная
производные поверхности по двум осям, нетрудно найти модуль градиента как
корень из суммы квадратов. В программе FemtoScan доступны три варианта
вычисления градиента: Gradient, Prewitt и Sobel. Эти варианты различаются матрицами
--
дифференцируемая функция. Зная
производные поверхности по двум осям, нетрудно найти модуль градиента как
корень из суммы квадратов. В программе FemtoScan доступны три варианта
вычисления градиента: Gradient, Prewitt и Sobel. Эти варианты различаются матрицами ![]() и
и
![]() . В таблице 3.4 приведены используемые матрицы.
. В таблице 3.4 приведены используемые матрицы.
Фильтр Laplace вычисляет лапласиан следующим образом:
![]() , где
, где